paper: Focal Loss for Dense Object Detection
Abstract
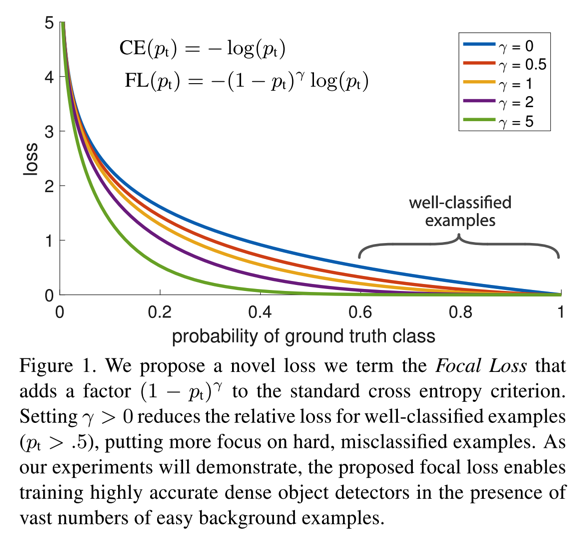
- 目前主流的目标检测方法,one-stage相较于two-stage的一个痛点就是样本分布的不平衡(目标和背景),导致one-stage虽然速度上有优势,但是精度却有所降低。因此,本文作者改写了传统的cross-entropy loss,分别增加了平衡正负样本的权重系数和平衡难易样本的系数,形成最终的focal loss。
- 同时,本文结合ResNet、FPN、FCN搭建了one-stage的RetinaNet,并用Focal Loss训练之,使得AP和Speed均明显提升。
- 如图:
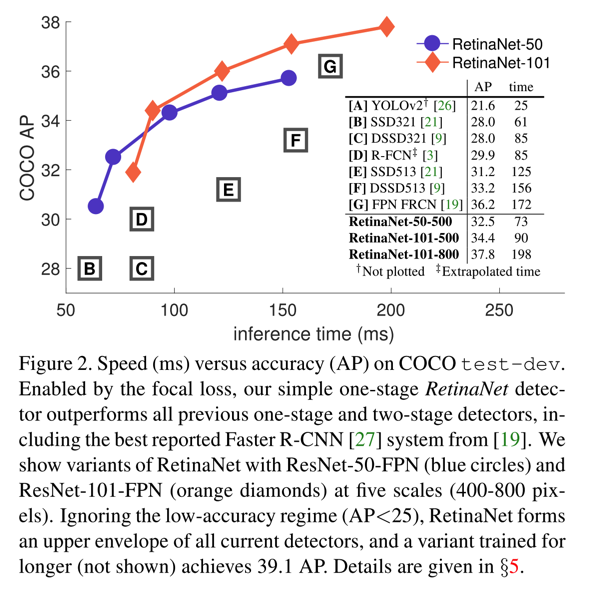
- 如图:
Details
- Focal Loss
- 目标检测中,样本主要包括前景(各类检测目标)和背景,其中背景的占比较多,导致类别不平衡,影响训练效果;再者,由于不同样本在训练过程中会有难易之分,即有些样本会很容易被分类(对应的置信度得分较高),有些样本则比较难(对应的置信度得分有限),如果在训练过程中同等对待,到整个训练的loss会被easy example占据太多,收敛效果有限
- cross-entropy loss
- $ CE(p,y) = \sum_{i}^{M} ylogp + (1-y)log(1-p) $
- 后续公式,以只有一个样本为例
- 针对第一点,作者在原来的二分类的cross-entropy loss上增加了alpha权重因子。即对正样本的loss增加alpha的权重,负样本的loss增加1-alpha的权重,论文实验的alpha=0.25,公式如下
- $ CE(p,y) =\left{\begin{matrix} - \alpha logp & y = 1\ - (1-\alpha) log(1-p) & otherwise \end{matrix}\right. $
- alpha-balanced cross entropy loss是为了能够调整少量样本的权重。相对于gamma,这个参数更为稳定,但是也需要根据gamma进行一定的调整,文中最好的0.25,应该是正负样本的比例
1:3的体现吧,这个比例可能也和真实的样本分布更吻合
- 针对第二点,对分类的预测概率增加影响因子gamma,论文实验的gamma=2
- $ CE(p,y) =\left{\begin{matrix} - \alpha (1-p)^\gamma logp & y = 1\ - (1-\alpha) p^\gamma log(1-p) & otherwise \end{matrix}\right. $
- 若对应目标样本,属于背景,则预测的概率P会很小,所以otherwise那一项也会很小
- 与OHEM策略相比,focal loss效果会更好,文中也有实验表明;可能是因为,OHEM在筛选样本时,是按照置loss进行排序,只筛选topk个,也就是easy example会全部丢弃掉
- FL的效果展示
- anchor标签
- RetinaNet中,对ancher的标签是one-hot的格式,即对于某个ancher,属于第i类,这K维度分类标签中,第i维为1,其他全部为0
- anchor的标签方式和RPN很像,根据IoU比值进行匹配,与gt的IoU大于0.5认为是目标,小于0.4认为是背景,0.4到0.5之间的全部ignore
- 每个anchor最多只能和一个gt匹配,而一个gt则可能对应了多个anchor
- RetinaNet
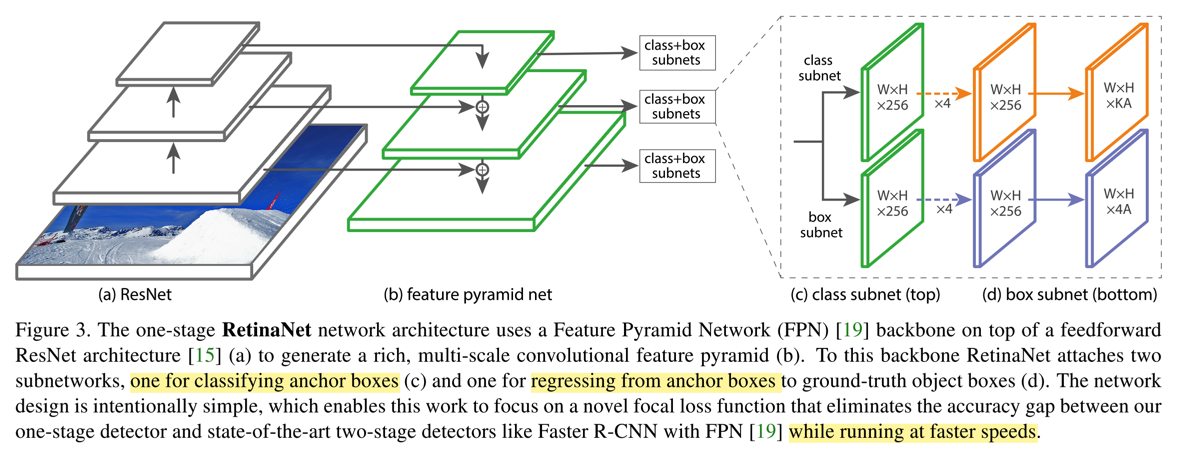
- RetinaNet的backbone网络是ResNet,再加上FPN,然后在FPN的每一个pyramid level之后添加两个FCN构成subnet,一个用于分类,一个用于回归,两者直接架构是一样的,但是参数不共享;框架如下:
- 分类的子网络,输入channel为C的FM,使用C个3*3的filter,每个后面接一个ReLU,然后再接KA个3*3的卷积,得到KA个W*H的FM,最后用sigmoid得到结果,相当于最后得到W*H的FM中,每个点的每个anchor的二进制分类(K代表类别数,A代表anchor个数)
- bbox回归的子网络,结构和上述的子网络一样,只是输出改为4A了
- RetinaNet的backbone网络是ResNet,再加上FPN,然后在FPN的每一个pyramid level之后添加两个FCN构成subnet,一个用于分类,一个用于回归,两者直接架构是一样的,但是参数不共享;框架如下:
- Trick
- 网络初始化时,引入一个先验(属于前景的概率)。因为前景的比例较少,在训练初期背景的loss容易占据主要部分;因此作者实验中,所有新增加的层(除了Retinal的subnet的最后一层)都按照bias=0、方差为0.01的高斯核初始化,而最后一层则使用bias=-log((1-pi)/pi)的方式初始化,其中pi为0.01,通过这种方式能够使得训练更加稳定